
Геометрия / Упражнения, решения/ А.П. Киселёв Геометрия
2. Доказать, что:
Если из середины каждой из равных сторон равнобедренного треугольника восставим перпендикуляры до пересечения с другой из равных сторон, то эти перпендикуляры будут равны.
Решение
Построим равнобедренный треугольник ABC и восставим перпендикуляры DE и FG из середин равных сторон.
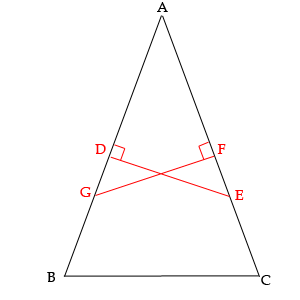
Образовавшиеся треугольники ADE и AFG равны. Так как равны их стороны AD и AF (они составляют половины равных сторон), у них общий угол A и углы D и F равны по построению. То есть они равны по двум углам и стороной меду углами.
Значит DE = FG .