
Геометрия / Упражнения, решения/ А.П. Киселёв Геометрия
1. Доказать, что:
В равнобедренном треугольние две медианы равны, две биссектрисы равны, две высоты равны.
Решение
Мы знаем что у треугольника, всегда есть три высоты, три медианы и три биссектрисы.
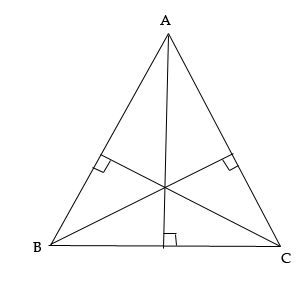
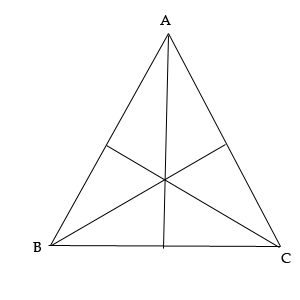
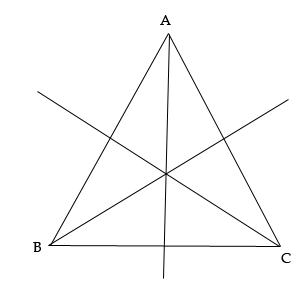
Мы не знаем равны ли они все между собой и в каком случае. Но то, что, в равнобедренном треугольнике две из них всегда равны, мы докажем.
Докажем равенство двух медиан:
Построим равнобедренный треугольник ABC и две его медианы CD и BE. Точку пересечения медиан (а она будет, это очевидно) обозначим буковой O.
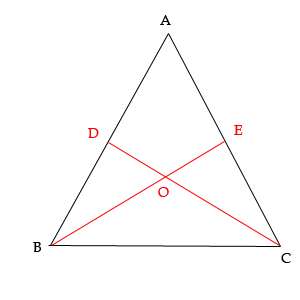
Образовавшиеся треугольники DBC и EBC равны. Так как сторона BC у них общая, стороны DB и EC равны, т.к. они составляют половины равных сторон BA и АC(по построению) и наконец мы знаем что у равнобедренного треугольника углы при основании равны. То есть треугольники DBC и EBC равны по двум сторонам и углу между ними. А раз они равны то и равны их стороны, то есть DС = EB.
Докажем равенство двух биссектрис:
В нашем треугольнике построим две биссектрисы CD и BE

Образовавшиеся треугольники DBC и EBC равны. Так как сторона BC у них общая, углы B и C равны (в р.т. углы при основании равны) и равны углы CBE и BCD т.к. они по величине составляют половины равных углов B и C (по построению). Тоесть треугольники DBC и EBC равны по двум углам и стороне между ними. Значит равны CD и BE.
Докажем равенство двух высот:
В нашем треугольнике построим две высоты CD и BE
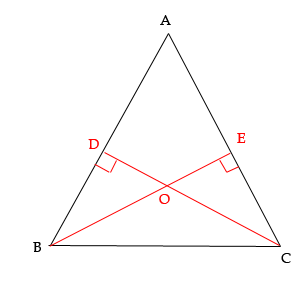
Образовавшиеся треугольники DBC и EBC равны. Так как сторона BC у них общая, углы B и C равны (в р.т. углы при основании равны) и углы D и E прямые(по построению). То есть треугольники равны как прямоугольные с соответственно равными острыми углами и соответственно равными гипотенузами. Значит равны CD и BE.