
Геометрия / Упражнения, решения/ А.П. Киселёв Геометрия
7. Доказать, что:
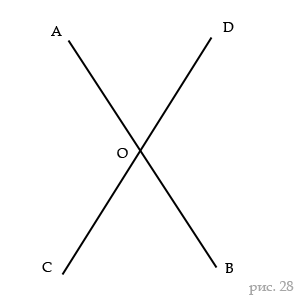
Если из точки O (рис. 28) проведём полупрямые AO, OD, OB, OC так, что угол AOC = углу DOB и угол AOD = углу COB, то OB есть продолжение OA и OD есть продолжение OC.
Решение
Сумма углов AOD, DOB, BOC, COA составляет полный угол (360°)(т.к. складывая все углы приходим к первому).
AOD + DOB + BOC + COA = 360°
Так как угол AOD = углу BOC и угол DOB = углу COA, то можно переписать
2AOD + 2DOB = 360° // поделим левую и правую часть на 2
AOD + DOB = 180°
Значит, OB есть продолжение OA.
Также пкажем что OD есть продолжение OC.
для этого перепишем выражение AOD + DOB + BOC + COA = 360° по другому:
2DOB + 2BOC = 360° // поделим левую и правую часть на 2
DOB + BOC = 180°
Значит, OD есть продолжение OC.