
Геометрия / Упражнения, решения/ А.П. Киселёв Геометрия
6. Доказать, что:
Если при точке O прямой AB (рис. 28) построим по разные стороны от AB равные углы AOD и BOC, то стороны их OD и OC составляют одну прямую.
Решение
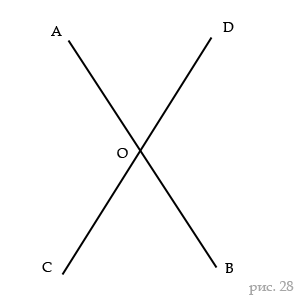
Углы AOD и DOB смежные т.к. сторона OB продолжает сторону AO и ОD общая сторона (по построению). Точно также углы AOC и BOC смежные. Так как сумма любых смежных углов равна 180° и углы AOD и BOC равны, то и углы AOC и DOB тоже равны (поскольку они дополняют равные углы до 180°). Получается что раз AOD и DOB в сумме равны 180°, то и сумма углов AOD и AOC тоже равна 180°. Из этого следует стороны CO и OD составляют прямую.