
Геометрия / Упражнения, решения/ А.П. Киселёв Геометрия
4. Доказать, что:
Медиана треугольника меньше его полупериметра.
Решение
Построим произвоьный треугольник ABC и его медиану BD.
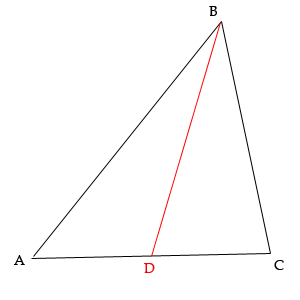
Мы знаем теорему о том что, одна из сторон треугольника всегда меньше суммы двух других сторон. По этому:
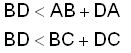
Сложим эти неравнества (cвойство неравенств в арифметике)

Так как DA + DC это AC, то перепишем:
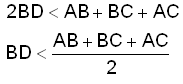
Из неравенства видим, что медиана меньше полупериметра. Таким же образом теорема доказывается для оставшихся двух медиан.